Here are a number of tried and tested technique for teaching work that learners find hard to learn.

Many low attaining learners have some (or all) of the following characteristics

1. 1. smaller working memory than their peers
   2. forget work they have learned more quickly than their peers
   3. "generalise after the fact" - that is they only generalise once they are comfortable with and have used and learned methods from many examples
      
   4. less able to transfer skills than their peers
   5. more easily "give up"

However we, as teachers can make situations to "work around" or overcome these characteristics so we can

1. 1. offer methods that require smaller working memory
   2. use retrieval practice or spaced learning so the memories we require learners to use are deeply embedded
   3. allow our learners to practice many examples and do not expect nor rely on the use of generalisations in our initial teaching
      
   4. help learners to transfer skills form one situation to another
   5. ensure most problems our learners encounter they can answer independently and accurately

Sharing the skills of a teacher "experienced in teaching low attaining learners" ...

Below are a number of pieces of advice for successful teaching of low attaining learners. Below this list of categories are descriptions which use one example to illustrate the points made and makes reference to the work arounds above. The links provide more examples and our "teaching Higher work to Foundation learners" videos. These videos are also referenced in the download a practise-learn pdf worksheet from learning resources. 

• scaffolding
• write long-windedly
• make more concrete
• reduce numerical demands (initially)
• with easily confused topics ...
• reduce shame in order to teach the 4 operations
• teach problem solving with/out a calculator 1st/2nd
• decode and use verbal clues
• explain why

scaffolding 

Using the timely practice system and mastery learning is a method of scaffolding over time. The layer are planned to make scaffolding simple and easy for the teacher. 

With scaffolding over time we are enabling stronger memories to be built up, due to retrieval practice or spaced learning. The memories on how to do easier skills will be available to the learners, often as a sequence of processes, these memories will be well embedded due to mastery learning and so require a smaller amount of  working memory. This allows more space in working memory to focus on the "one small bit harder" of the new learning.

For example to "Work out 15% of £82" without a calculator. If learners already have deeply embedded the learning of how to work out 10% and 5% then the "one small bit harder" is to decide - how can I split up 15% into two percentages I already know how to work out". Without the strongly embedded learning of the 10% and 5% the process becomes much more difficult to hold in memory and to think about, both of which require short term memory capacity.

By the carefully designed scaffolding within the way that the layer are built up we 

1. 1. offer methods that require smaller working memory
   2. use retrieval practice or spaced learning so the memories we require learners to use are deeply embedded
   3. callow 
      
   4. help learners to transfer skills form one situation to another
   5. ensure most problems our learners encounter they can answer independently and accurately

See the scaffolding link for more examples.

write long-windedly

This is the opposite of simplify - it helps learners both understand and remember their work and also helps learners "get" why mathematicians are always compacting.

For example with "Simplify b⁵ x b³" initially we get learners to "write it out long-windedly first" that is b x b x b x b x b x b x b x b. Ultimately we want the learner to imagine the method of writing the problem out "long-windedly" to ensure they arrive at a secure and accurate answer. Insisting learners write out their work long-windedly when they make an error with questions like this ensures understanding as to why we add the indices rather then learners trying to remember "is it + or x ?".

For some learners with strong memories, and who generalise quickly the "long-winded" approach is un-necessary but for low attaining learners we

1. 1. offer methods that require smaller working memory
   2. use retrieval practice or spaced learning so the memories we require learners to use are deeply embedded
   3. allow our learners to practice many examples and do not expect nor use generalisations in our initial teaching
   4. d
   5. ensure most problems our learners encounter they can answer independently and accurately
      
      

See the write long-windedly link for more examples.

make more concrete

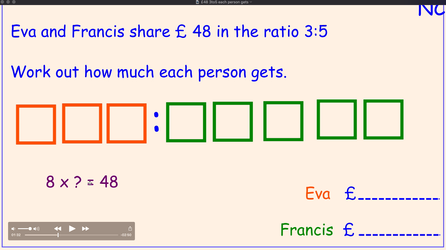
An abstract notion such as ratio is because it is hard to "hold on to mentally" so takes up a lot of working memory (and of course it is hard because it involves multiplying, dividing and finding a scale factor) - so enabling learners to have a concrete model which they can put on the page, and not need to hold in working memory is hugely beneficial. With the problem

First we encourage learners to draw out the ratio as boxes and label the boxes - moving from the abstract to the concrete. If we further provide a rational as to why Eva gets less than Francis (such as Eva worked for 3 hours and Francis worked for 5) then we have removed that worry form our learners minds.

In making problems more concrete we

1. 1. offer methods that require smaller working memory
   2. b
   3. c
   4. d
   5. ensure most problems our learners encounter they can answer independently and accurately

See the make more concrete link for more examples.

reduce numerical demands (initially)

When teaching a topic, which will ultimately demand a high level of numeracy skill(s) and also some complexity of method it is beneficial to teach learners only with examples which are carefully chosen to make the numeracy demands low whilst the method is learned.  

An example of this is teaching learners to find the product of prime factors of a number. First learners meet cases where only dividing by 2 and 10 is required. Once the method is fully mastered then more numerical difficulties can be added. In this case the next stage is needing to divide by 9 (when the 9's fingers trick can be used but the learners must also remember to write 9 as a product of its factors); the next where dividing by 3 and 5 are required and finally only for those learners who master HCF and LCM would learners meet problems where they had to systematically try other prime numbers to find all the prime factors. 

In developing timely practice, we have been able to spend time planning carefully which numbers (to find the prime factor of) should go in each stage and so allow the teacher to easily scaffold her teaching. So within the layer we 

1. 1. offer methods that require smaller working memory
   2. use retrieval practice or spaced learning so the memories we require learners to use are deeply embedded
   3. allow our learners to practice many examples and do not expect nor use generalisations in our initial teaching
   4. d
   5. ensure most problems our learners encounter they can answer independently and accurately

See the reduce numerical demands (initially) link for more examples.

with easily confused topics ...

With two concepts are ubiquitously confused by learners such as area and perimeter, we know that after teaching one carefully - to what seems like mastery - when the other is introduced most learners will become confused. We encourage learners to embrace this confusion and encourage them to self reflect 

• if this question was about finding the area - what would I have to do?
• if this question was about finding the perimeter - what would I have to do?

and then finally to think

• OK this question is area (perhaps they use the clue on the answer line " .... m²  - so I want to work out the number of squares") to give their answer confidently

If learners believe that most people run into the confusion that they have encountered, and that there is a logical way through the problem, and that a pause for thought leads to an accurate answer and most importantly the learners encounter as many instances in their timely practice assignments as required to accurately match the name of the concept with the concept then the teaching and learning process will succeed.

When designing the lay out of the questions we ensure that the questions looked exactly the same apart from the essential key differences - in this case the word area or perimeter and the units on the answer line. We find learners do focus on mastery, if for no other reason that they become "bored" by getting their answers wrong and then "challenged" to get the questions correct. 

We encourage teachers to get learners to reflect on situations where the learner has succeeded in overcoming this confusion before such as

"Remember when you used to be confused between area and perimeter? 

... now you get these correct every time, well,

I think it will be the same with  b x b x b and b + b + b"

This is more than just encouragement, the teacher is getting the learner to recall the "feeling of pride in a job well done" and establishing both the learner and the teachers belief in a "growth mindset". 

So by accepting that learning of some topics will interfere with the learning of other topics and embracing this - we are able to help the learners to match the ideas and the names attached to those ideas. To summarise we 

1. 1. a 
   2. use retrieval practice or spaced learning so the memories we require learners to use are deeply embedded
   3. allow our learners to practice many examples and do not expect nor use generalisations in our initial teaching
      
   4. help learners to transfer skills form one situation to another
   5. e
      
      

See the with easily confused topics ... link for more examples.

reduce shame in order to teach the 4 operations

Our topics add NC, subtract NC, multiply - pdf & mp4, divide - pdf & mp4  are designed so that it is hard, with a casual glance, to decide how hard any particular question is. Due to the nature of retrieval practice or spaced learning any learner might find the odd very easy question in their timely practice assignment -  in both these ways the potential to feel shame is reduced.

Our experience is that "no calculator word problems" are one of the areas that low attaining learners in KS4 are least likely to "have a go at" probably because they have been "failing" at the 4 operations for the longest. Teachers can offer the possibility that "perhaps it is not that learners can't do +, - x and ÷ but that they can't recognise which operation to choose". This somehow shifts the shame - suddenly it's not the fault of the learner who hasn't been able to learn these skills for 7 or more years, now it is the fault of - I usually like to blame the national curriculum (if a scapegoat needs to be found) - for having not given the learners enough opportunity to know which operation to use.

Once shame is less likely to be felt and since each topic is so finely divided into layers (see scaffolding) learners can ordinarily do at least one layer in add NC and multiply - pdf & mp4 - although admittedly not strictly in a "Gove approved" method. In fact "Gove approved" methods (which can be generalised as paper saving methods) have high requirements for working memory so are generally best avoided. Our experience is that if teachers use mastery learning to teach numeracy skills, (and focus on memory saving methods rather than paper saving methods) then learners can feel "safe and secure enough", to build up  "forgotten or never learned" numeracy skills.

Warning: this method is a "fake Gove method"

In teaching the 4 operations we

1. 1. offer methods that require smaller working memory
   2. use retrieval practice or spaced learning so the memories we require learners to use are deeply embedded
   3. allow our learners to practice many examples and do not expect nor use generalisations in our initial teaching
      
   4. help learners to transfer skills form one situation to another
   5. ensure most problems our learners encounter they can answer independently and accurately

See the reduce shame in order to teach the 4 operations link for more examples.

teach problem solving with/out a calculator 1st/2nd

It is helpful to unlink in our minds as teachers the difficulty of the numeracy involved in a problem and the difficulty of mathematical process involved in a problem. I'm sure most maths teachers can think of 

• a learner who is especially weak at numeracy but especially strong at maths problem solving and conversely
• a learner who is especially strong at numeracy but especially weak at maths problem solving.

If we assume that low attaining learners are atypical of most learners, then we shouldn't wait for our learners numeracy skills to be at a certain level before we introduce them to maths problem solving however we should wait for our learners to be confident at a certain level of maths problem solving before we introduce them to harder maths problem solving (mastery learning).

In learners early problem solving in maths, using a calculator is a hindrance to solving word problems.

However once learners can match the 4 operations with the wording of a question then using a calculator can help a learner to learn harder problem solving skills. 

So using or not using a calculator to solve word problems enables us to 

1. 1. offer methods that require smaller working memory

   2. b

   3. allow our learners to practice many examples and do not expect nor use generalisations in our initial teaching
   4. help learners to transfer skills form one situation to another 
   5. e

See the teach problem solving with/out a calculator 1st/2nd link for more examples.

decode and use verbal clues

Sometimes we need to help learners decode the words we use in maths. A simple example is the link between long and length, wide and width and high and height. By showing learners how we take the short word and change and extend the words, makes the link clear to learners. 

long → loength

wide → wideth

high → height

By using these tricks we can 

1. 1. offer methods that require smaller working memory
   2. use retrieval practice or spaced learning so the memories we require learners to use are deeply embedded
   3. c
   4. help learners to transfer skills form one situation to another
   5. ensure most problems our learners encounter they can answer independently and accurately
      
      

See the decode and use verbal clues link for more examples.

explain why

Sometimes it helps learners to know "why" processes work - but sometimes this makes learning new processes just too hard. 

So the reason why the "trick for multiplying fractions" works is helpful but perhaps the "trick for dividing one fraction by another" is not.

Offering reasons why is helpful if it helps learners follow a process that would otherwise seem arbitrary, when the reason gives more meaning, but only if the reason is no more complicated than the process being learned. So if working memory load is decreased or memory can be retained longer because it is attached to something that is already learned it can be helpful.

Explaining why can have any of these benefits, but any particular instance is unlikely to have all of these benefits.

1. 1. offer methods that require smaller working memory
   2. use retrieval practice or spaced learning so the memories we require learners to use are deeply embedded
   3. allow our learners to practice many examples and do not expect nor use generalisations in our initial teaching
      
   4. help learners to transfer skills form one situation to another
   5. ensure most problems our learners encounter they can answer independently and accurately
      
      

See the explain why link for more examples.