One of a number of tried and tested technique for teaching work that students find hard to learn found in teaching tricks and tips
Making any problem more concrete makes it take less working memory - and that is one of the best ways of enhancing the learning of low attaining students.
On this page are a number of examples where we expect our students to record on their page, in a concrete way, perhaps with boxes, function machines etc to enable the student to need to hold less in working memory and so free up enough working memory to continue to solve the problem.
If we as teachers think of a way in which our working memory isn't sufficient and what we do about this, this will help in our teaching. At every step of problem solving we could think, what am I remembering? and would all my students be able to hold all of this in their heads, without something slipping out?.
everyday situation when working memory isn't enough
Imagine you are getting a round of drinks in, could be a coffee run or a pub.
For 3 people you can probably remember what they all want Anja wants ... Bihl wants ... Carli wants ...
However how about 6 people? ... 11 people ... probably not, so what we do is make a list - we have now "freed up" our short term memory and can now concentrate on getting the correct milk and sugar in the correct mugs.
low attaining students in maths have less working memory than their peers
I personally suspect that smaller working memories and shorter long term memory retention is causal to low attainment ... but I don't know any way to prove this (ethically) than try to improve low attaining students effective memory capacity and strategies to increase long term memory intention. True or not, giving students strategies to need less working memory in problem solving enables better attainment outcomes.
Giving students more concrete methods "frees up" working memory for often numeracy, so will generally make students more accurate.
One of the problems with giving more concrete methods is that it often goes against giving "paper saving methods", which have come to be considered to be standard methods (for more on this see the long multiplication and long division sections below).
The plan for this page is to build up examples and include links to "teaching Higher work to Foundation students" videos and more easy on the eye student "remind-me" videos. For now though here is a list of situations where we have found asking students to make it more concrete has helped.
use boxes
ratio
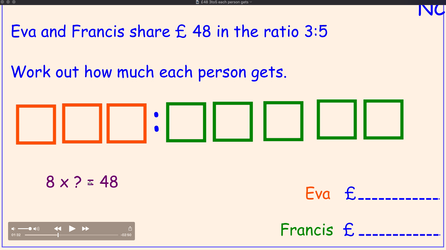
An abstract notion such as ratio is because it is hard to "hold on to mentally" so takes up a lot of working memory (of course it is also hard because it involves multiplying, dividing and finding a scale factor) - so enabling students to have a concrete model which they can put on the page, and not need to hold in working memory is hugely beneficial. With the problem
ratio: £48 3to 5 (remove this picture once video is available)
Note we encourage students to draw out the ratio as boxes and label the boxes - moving from the abstract to the concrete.If we further provide a rational as to why Eva gets less than Francis (such as Eva worked for 3 hours and Francis worked for 5) then we have removed that worry form our students minds. Now we have "freed up" working memory so students can concentrate on solving the rest of the problem.
This method can be adjusted for more complex situations
- ... how much more money does Francis get than Eva
- Francis gets £10 more than Eva, how much ....
- Eva gets $240 how much does Francis get
- A piece of copper pipe is divided in the ratio 3:5
- A piece of copper pipe is divided in the ratio 1:3:5
other situations to use boxes
- fraction of
- fraction of: fraction of the thing
- fraction of: LESLEY rerecord fraction of the number
- convert between a ratio and a fraction
- FD%RasaFD%R: ratio3to4Fraction
- FD%RasaFD%R: Fasaratio
use function diagrams
- solve
solve: 4e + 22 = 70 (where the function machine is writing out all the things that happen to e long-windedly)
solve: m - 6 = 8 (where the function machine is writing out what happens to m long-windedly)
- change units
- changeUnits: m2cm
- changeUnits: grams2kg
- exchange rate
start with a standard way to write out the first step
- simple probability - write out all the possible outcomes
- % of CALC problems - write word problem in maths
- percent CALC: 17%
- % of NC problems - start by writing 100% = ...
- percent NC: 2% of £560
- percent NC: 10% of £4.60 LESLEY record
- expand
- expand: number(outside a bracket) algebra 5(x + 3)
- expand: just a letter(outside a bracket) x(x-3) algebra
- expand: (a bracket squashed)(next to another bracket) exp&simp (m + 3)(m+2)
- BIDMAS problems, write out the problem (with more space and write out BIDMAS and then again in signs)
- pictograms, write the amount inside or below each picture
0 Comments